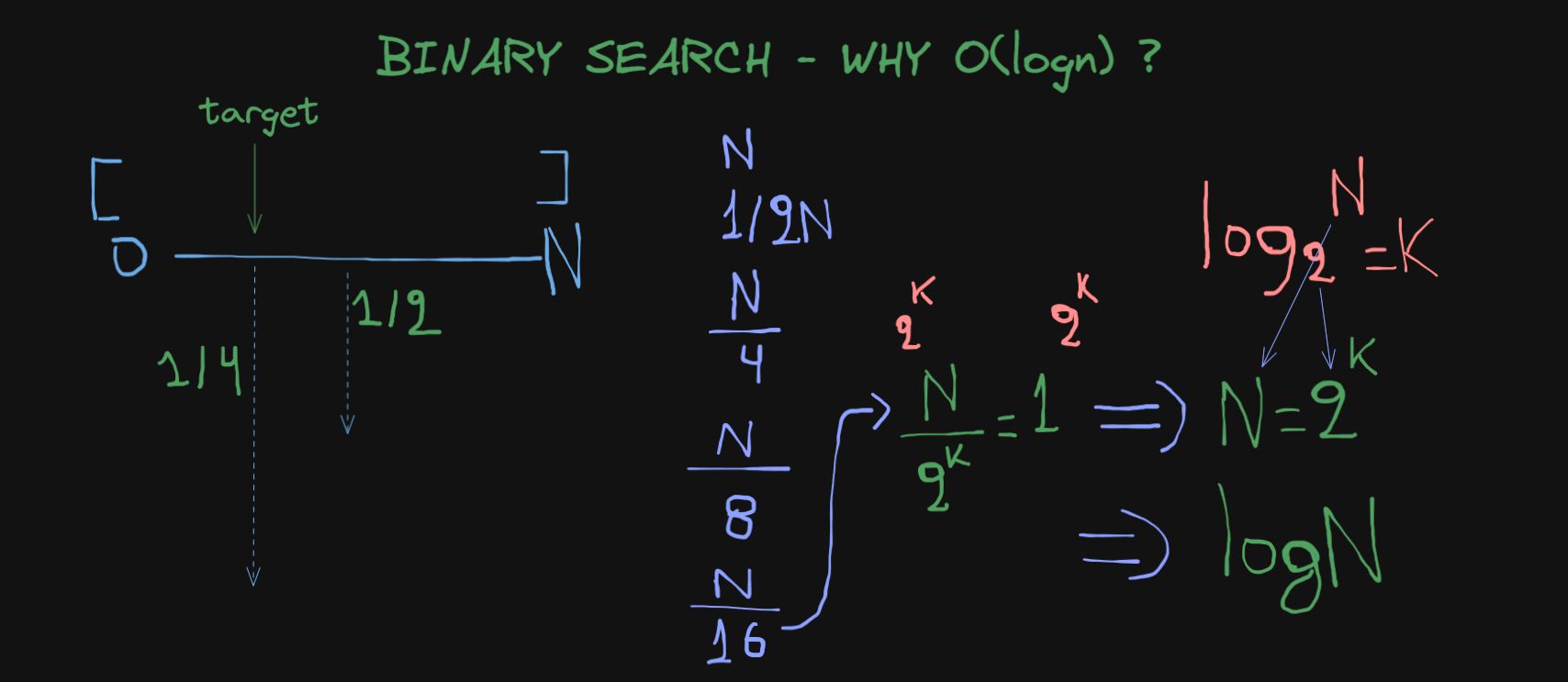
Have you ever wondered why the time complexity of some algorithms, for example Binary Search, is O(logn)?
What does this mean exactly and how did we come up with logn?
In case you are not aware of it, Binary Search is a searching algorithm used in a sorted array by repeatedly dividing the search interval in half.
As we are splitting the array in halves, it keeps get shorter and shorter until a certain condition is met: (green equation)
By multiplying both parts with 2^k we get N = 2^k and we know that log of base 2 of N equals k. So, we are halfing the array logn amount of times.
Where did we get that condition (N / 2^k = 1) from?
Imagine an array that has 4096 elements: 4096 / 2 = 2048 2048 / 2 =1024 1024 /2 = 512 512 / 2 = 256 256 / 2 = 128 128 / 2 = 64 64 / 2 = 32 32 / 2 = 16 16/ 2 = 8 8 / 2 = 4 4 / 2 = 2 2 / 2 = 1
So log4096 = 12, and how many steps did we do to get to 1 ? We performed 12 steps. By that time you reach 1, you will know whether or not the value you are looking for is in the array.
Why is it called Binary Search? Well, because in every step you either have found what you are looking for or you do a binary case decision - either going left (continue search in the left half) or going right (continue search in the right half), depending on if what you search for is smaller or larger than the current value (middle position of the half).
Finally, if the input halves at each step, its likely O(logN) or O(NlogN) depending on if you're scanning the input or not. We are not scanning anything we are only looking at a value and dividing by half.